In this blog post I want to discuss how the tSNR in sub-millimeter fMRI can be substantially improved by optimizing the GRAPPA regularization. Adjusting one single GRAPPA reconstruction parameter can almost double the tSNR of your fMRI time series. With almost no penalty.
Acknowledgements
I want to thank Jonathan Polimeni for making me aware of the additional GRAPPA parameters that discussed here and I want to thank him for referring me to the relevant literature. Scanning together with Jonathan for 30 min (June 2nd at the 7T in Magdeburg), I learned more about how to improve my data than the 2 years before that.
I also want to thank Sean Marrett for the extra development scan time to explore the effect of the GRAPPA regularization on fMRI signal stability.
Thanks to Yuhui Chai for being my brave volunteer to test the different reconstruction parameters.
I thank Philipp Ehses and Rüdiger Stirnberg from the DZNE, Bonn for explaining how this works in IcePat on VE (last section).
Optimizing GRAPPA reconstruction parameters for fMRI
MRI is used in very different contexts: anatomical vs. functional imaging, head vs. body imaging, clinical vs. high-field imaging, low-resolution vs. high-resolution imaging. It is fully established to use different acquisition setups for the specific application (i.e. different sequences and different hardware). However, I found it surprising that this is not the case for the reconstruction pipeline. No matter if you use GRAPPA for body imaging at 3T or if you use GRAPPA for sub-millimeter fMRI, the same GRAPPA algorithm parameters are used. This is the case, even-though the different applications have very different needs. In 3T clinical imaging, the imaged need to be reconstructed within a few milliseconds with a spatial homogeneous signal. However, sub-millimeter fMRI is not limited by few extra seconds of reconstruction time and small variations of spatial signal intensities. Instead, sub-millimeter fMRI is limited by the temporal stability.
For unfortunate reasons, the default GRAPPA reconstruction parameters seem to be adjusted (from SIEMENS?) as a gross compromise to work across all possible applications. This means, however, that there is a lot of room for improvements for any given specific application. GRAPPA parameters can be optimized for sub-millimeter fMRI to double the tSNR differently than 3T clinical body MRI.
This mean that it can be beneficial to adjust the GRAPPA parameters for sub-millimeter fMRI. E.g. making a tradeoff to double the tSNR for a 5% increase of spatial inhomogeneities and a 1 sec longer reconstruction time, can be considered worthwhile.
In my test experiments (below) with submillimeter fMRI at 7T with FLASH and FLEET GRAPPA ACS, I conclude that it can be very beneficial to increase the χ-regularization parameter up to a factor of 1000 with only minimal amplifications of the artifact level. This improves the tSNR by a factor of 50-100%.
Introduction to GRAPPA
GRAPPA acceleration is vital to achieve reasonable echo times and efficient data acquisition in high-resolution fMRI on SIEMENS systems. However, it comes along with a big set of scan/reconstruction parameters. It is not very straight forward to understand their inter-dependencies and it its cumbersome to adjust them optimally for any given protocol. Some of the GRAPPA parameters have a big effect on the noise-level and artifact level of the final fMRI time series. Hence they should be chosen with care and optimized for every specific protocol.
In previous blog posts, I already talked about the GRAPPA ACS acquisition scheme and the GRAPPA kernel size. In this post, I want to discuss the effect of the parameters used in the GRAPPA fitting procedure.
Background
In GRAPPA fMRI, the missing data-points of an under-sampled k-space are filled by interpolating the signal strengths from neighboring acquired data points. This interpolation is done as a simple linear weighted sum. The collection of weight factors are often referred to as GRAPPA kernel. It can be written as a three dimensional matrix kernel_size_x ⊗ kernel_size_y ⊗ number_of_coils.
Filling the missing k-space lines has often been described in the matrix notation. The GRAPPA kernel fit can then be seen as a matrix inversion (see below).
SIEMENS implementation of GRAPPA
I found it very hard to figure out how this works exactly in the SIEMENS reconstruction pipeline. While I don’t know anybody who could give me access to the SIEMENS course code of the GRAPPA reconstruction, I can try to reverse-engineer what it does.
There is a 10-year old Masters thesis from Matthias Schneider from the computer science department of the University of Erlangen. It seems that Matthias did an internship with Michael Peyerl, Gerald Mattauch, and Swen Campagna from Siemens Medical Solutions. Based on his acknowledgement section, he had access to the source code of the GRAPPA reconstruction ICE functor GrappaFindWsImproved. Hence, his pseudo code snippets and his vocabulary of the basic algorithms parameters are likely close to the SIEMENS implementation. His thesis is actually not really supposed to be dealing with the GRAPPA reconstruction. Instead, its about optimized matrix multiplications with GPUs in CUDA. However, in his introductory sections, he describes the motivation for his work in the light of GRAPPA reconstructions. These “introduction sections” are the interesting parts for me, where we can learn how SIEMENS algorithm of GRAPPA works.

In the code snippets, Matthias describes the most important free parameters of the GRAPPA reconstruction, that the user has access to: η, χ, and κ.
For more information about the naming convention and about the background of what every single parameter means, see section 2.6 and 4.1 of his thesis (its in English).
Parameter η: metric of the matrix normalization
- Matthias Schneider calls this the parameter for normalization.
- I believe it refers to the Xbuilder parameter GrappaArtifactReduction.
- In the ICE functor GrappaFindWs, this parameter is called ArtifactReduction.
- The default parameter is 1. This value would refer to an Euclidean normalization of the exponent “-1/2”. I.e. a conventional square root.
- This parameter is used in line 26 Matthias’ pseudo code snippet.
- I found that this parameter has a small effect on the GRAPPA artifacts in sub-millimeter fMRI. While it seems more relevant for anatomical imaging, it does not really affect the data quality of 7T sub-millimeter fMRI.


Parameter χ: metric of regularization
- Matthias Schneider calls this the parameter for regularization.
- I believe it refers to the Xbuilder parameter GrappaNoiseReductionI.
- In the ICE functor GrappaFindWs, this parameter is proportional to the parameter NoiseReductionI. I believe the NoiseReductionI term in the ICE functor GrappaFindWs refers to the proportional factor λ.
- The default parameter is 1. For my data (32ch coil and GRAPPA 3), this refers to a λ factor of 0.0001.
- In my experience, this parameter is the most crucial parameter to adjust for every scan protocol. Not optimizing it and using the default, can result in 50% lower tSNR. Too high parameters can result in overfitting and large GRAPPA ghosts.
- This parameter scales the noise term in of the residuals in the matrix inversion (Grappa-kernel fit). See equation 2.8 of Matthias’ thesis.
- This parameter is used in line 46 Matthias’ pseudo code snippet.


Example from another participant.
Data are taken from this study.

- Raw single time point image quality of the same dataset reconstructed with different regularization factors.


Parameter κ: metric of power clipping
- Matthias Schneider calls this the parameter for power clipping.
- I believe it refers to the Xbuilder parameter GrappaNoiseReductionII.
- In the ICE functor GrappaFindWs, this parameter is proportional to the parameter NoiseReductionII.
- The default parameter is 0.
- In my experience, this parameter has almost no effect almost on the final image quality.
- This parameter is used in line 4 Matthias’ pseudo code snippet.
Access to GRAPPA reconstruction parameters on VB17
Access via Xbuilder
All the GRAPPA parameters can be seen and adjusted at the scanner as follows:
- Start “xbuilder” (Ctrl+Esc and run xbuilder)

- Open the file c:/MedCom/config/Ice/IceConfig.evp
- Find parameter ICE/CONFIG/iPAT/GrappaArtifactReduction, GrappaNoiseReductionI, and GrappaNoiseReductionII.

Note: The file IceConfig.evp is overwritten every time a new ‘patient’ is registered. Hence, if you mess around in IceConfig.evp, there is no danger that you affect other people scanning after you. However, it also means that you should always apply your changes after your patient is registered.
Note: The GRAPPA parameters the current IceConfig.evp file are also used for Retro-Recon. This means that when you want to RetroRecon an old dataset while a different patient is currently registered. The setup of the current patient will be used. This feature also allows you to reconstruct the same date with multiple GRAPPA-algorithm parameters. Just change IceConfig.evp in the current patient and any data will be reconstructed with the current set of parameters during RetroRecon in Twix.
Note: The GRAPPA regularization is automatically switched of, if the number of GRAPPA reference lines exceeds 48 (This is the famous Heindemann-factor). E.g. use 45 GRAPPA reference lines instead.
How to find out which regularization was used
Very often you would like to find out which GRAPPA-parameter were used. And/or you want to double check whether your manually changed kernel-size was properly applied. You can check the used GRAPPA-kernel size in the Twix data as follows:
- Start Twix (Ctrl+Esc and run twix)

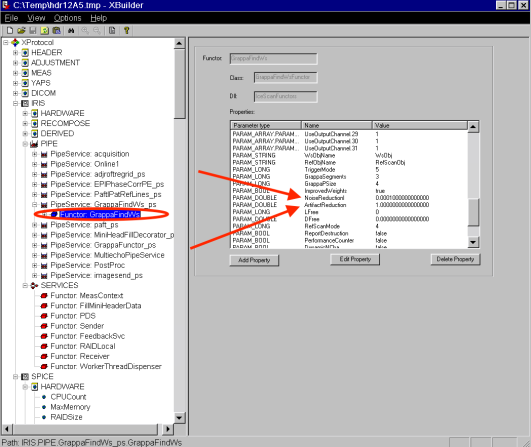
- Select the dataset in the left panel (red), open RetroRecon (blue), and click on edit (green).

- The used GRAPPA parameters can be seen in -> XProtocol-> IRIS -> PIPI -> GrappaFindWs -> Functor (black arrow).
Access to GRAPPA reconstruction parameters on VD/VE, when using IcePat
Addendum based on input from Philipp Ehses
For scanners running on VD and VE (e.g. Terra), more sequences routinely use the IcePat GRAPPA reconstruction instead of the older PAT^2 only. While the PAT^2 does 3D-GRAPPA reconstruction consecutively in the two dimensions as described here, the newer IcePat does it simultaneously in two dimensions as described here.
Commonly, you can select which of the two procedures you use in the Resolution/iPAT card of the protocol editor of your sequence.

If you are using IcePat, the way how you adjust the regularization strength is slightly different than described above. Namely you need to follow the steps below:
- You execute xbuilder in the terminal.
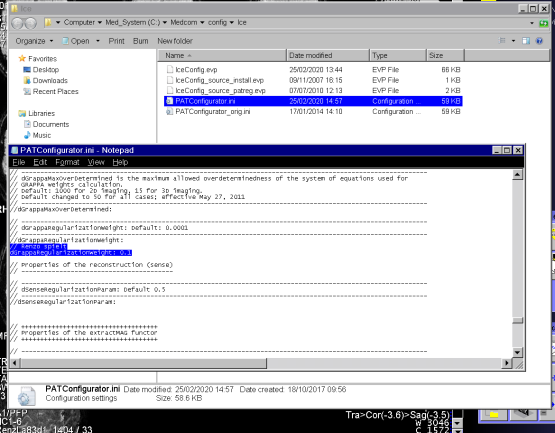
- You open the file C:/MedCom/config/Ice/IceConfig.evp and navigate to the parameter ICE/CONFIG/iPAT/IcePATReadIniFile.
- You change the value to 1

- You open the file C:/MedCom/config/Ice/PATConfigurator.ini and navigate to the place where dGrappaRegularizationWeight is set.
- You change the parameter from 0.0001 to 1.0 via dGrappaRegularizationWeight: 1.0. Note that you need to change it back to the default after you are done with your experiments. The file is not resetted after at the registration of a new “Patient”.
Similarly to as described above, the regularization strength can have significant benefits for fMRI time series at the cost of GRAPPA ghosting level.






I really appreciate your efforts to helping us understand more of what’s going on ‘behind the scenes’ in our reconstructions – thanks! As you increase the regularization – and get more tSNR – I would be concerned that you might also be trading off against independence of the signals – and sensitivity to small changes in signal (a static image has infinite tSNR….). Have you looked at this too?
LikeLiked by 1 person
Hi Daniel,
Sure, I am also concerned that its possible to over-regularice it.
E.g. in the extreme case the missing k-space lines are no longer interpolated but the lines are basically just copied versions of its neighbours (extreme case of trading off against independence). In this case, the resulting image will look like there is not GRAPPA unaliasing going on. And the GRAPPA ghosts would be just as big as the signal itself. I belive in the case of Chi=100000 (above), this is the underlying problem.
I haven’t tested it myself but I belive the point of diminishing returns (the point of over-regularization) will be different for different FOVs and different RF-coils.
So, one might need to optimize the regularization strength on a protocol-by-protocol basis.
Its just yet annother parameter that is worth to be included into protocol setup.
Given the under-regularization of the default parameter, I belive there is a lot to gain before we pay a price in loosing independence.
I intend to do additoinal fMRI tests quaintifying the functional signal changes in the next week and I’ll include it in the post.
Renzo
LikeLike